Question

Find the area of each regular polygon. Round your answer to the nearest tenth if necessary.

Answer 1

*I am assuming that the hexagons in all questions are regular and the triangle in (24) is equilateral*

(21)

Area of a Regular Hexagon:
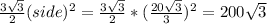`(3√(3))/(2)(side)^(2) = (3√(3))/(2)*((20√(3) )/(3) )^(2) =200√(3)` square units

(22)

Similar to (21)

Area =
`216√(3)` square units

(23)

For this case, we will have to consider the relation between the side and inradius of the hexagon. Since, a hexagon is basically a combination of six equilateral triangles, the inradius of the hexagon is basically the altitude of one of the six equilateral triangles. The relation between altitude of an equilateral triangle and its side is given by:

`altitude=(√(3))/(2)*side`

`side = (36)/(√(3))`

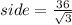
Hence, area of the hexagon will be:
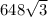`648√(3)` square units

(24)

Given is the inradius of an equilateral triangle.

`Inradius = (√(3))/(6)*side`

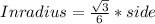
Substituting the value of inradius and calculating the length of the side of the equilateral triangle:

Side = 16 units

Area of equilateral triangle =
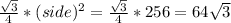`(√(3))/(4)*(side)^(2) = (√(3))/(4)*256 = 64√(3)` square units