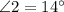1 Answer

Kantharis · Answer 1 · 2021-09-23T01:38:49+0000

The measure of angle 2 is
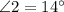
$\angle 2=14^(\circ)$

Step-by-step explanation:

Given that
$\angle 1$ and
$\angle 2$ are complementary angles.

Also, the measure of angle 1 is
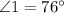
$\angle 1= 76^{\circ$

We need to determine the measure of
$\angle 2$

Since, we know that the complementary angles add up to 90°, then the angles
$\angle 1$ and
$\angle 2$ add up to 90°.

Thus, we have,

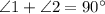
$\angle 1+\angle 2=90^(\circ)$

Substituting the value of
$\angle 1$ in the above expression, we have,

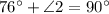
$76^(\circ)+\angle 2= 90^(\circ)$

Subtracting both sides by 76°, we get,

$\angle 2 = 90^(\circ)-76^(\circ)$

Simplifying, we have,

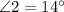
$\angle 2 = 14^(\circ)$

Thus, the measure of angle 2 is
$\angle 2=14^(\circ)$

Please log in or register to add a comment.