Question

Let f(x) = x^2 +3.

Let g(x) = (x+6)^2 + 3.
Which statement describes the graph of g(x) with respect to the graph of f(x)?​

Answer 1

It is translated left 6 units

Explanation:

I will help you understand graphing a function.

1. Each part in the equation represents how the graph will look.

In the first equation you have an
`x^(2)` and the number 3.

In the second equation you have an
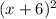`(x + 6)^(2)`and that same number 3.

2. First look at the variable: the
`x^(2)` tells us that both of these functions are positive quadratics opening up

3. The number on the outside tells you where the function is located on the y-axis (vertical movement)

Both equations have the number 3 so the graph will be 3 units high

4. The number on the inside with the variable determines the horizontal movement of the graph

The second equation has a (x + 6)

It might be confusing to think that since its addition the graph should go to the right but it actually goes to the left.

A good saying, I keep in my head is that parenthesis lie (x + 6) really mean 6 units to the

I will also add an image of the graph of the function below.

Answer 2

translated left by 6 units

Explanation:

Given f(x) then f(x + a) is a horizontal translation of f(x)

• If a > 0 then shift left of a units

• If a < 0 then shift right by a units

g(x) = (x + 6)² + 3

Indicating a shift of f(x) to the left by 6 units