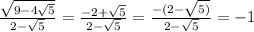Answer:
a)
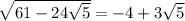
b)
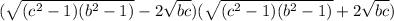
c)
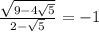
Explanation:
We want to simplify
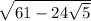
Let :
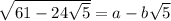
Square both sides:
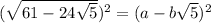
Expand;
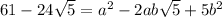
Compare coefficient:
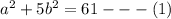
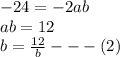
Solve simultaneously,
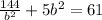
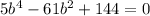
Solve the quadratic equation in b²
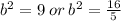
This implies that:
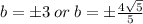
When b=-3,
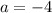
Therefore
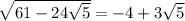
We want to rewrite as a product:
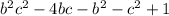
as a product:
We rearrange to get:
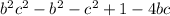
We factor to get:
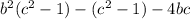
Factor again to get;
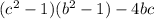
We rewrite as difference of two squares:
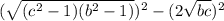
We factor further to get;
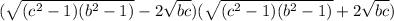
c) We want to compute:
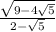
Let the numerator,
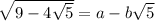
Square both sides;
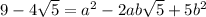
Compare coefficients;
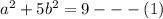
and
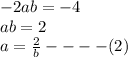
Put equation (2) in (1) and solve;
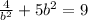
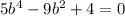
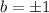
When b=-1, a=-2
This means that:
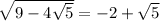
This implies that: