foci of
 is
is
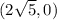 . correct option a.
. correct option a.
Explanation:
Complete equation of Hyperbola for the above question is x2/16-y2/4 = 1 or
 , Simplify each term in the equation in order to set the right side equal to 1 . The standard form of an ellipse or hyperbola requires the right side of the equation be 1 . This is the form of a hyperbola. Use this form to determine the values used to find vertices and asymptotes of the hyperbola:
, Simplify each term in the equation in order to set the right side equal to 1 . The standard form of an ellipse or hyperbola requires the right side of the equation be 1 . This is the form of a hyperbola. Use this form to determine the values used to find vertices and asymptotes of the hyperbola:
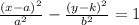
a=4 , b = 2, h = 0 , k= 0
Find the distance from the center to a focus of the hyperbola by using the following formula:

Substitute the value of a and b in the formula.
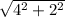 =
=

The first focus of a hyperbola can be found by adding c to h
(h+c,k)
Substitute the known values of h , c , and k into the formula and simplify:
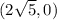 . ∴ foci of
. ∴ foci of
 is
is
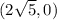 . correct option a.
. correct option a.