Step-by-step explanation:
Here we know that an internet service provider is implementing a new program based on the number of connected devices in each household. Currently, customers are charged a flat rate of $175 per month. Assuming just a month, we can write a constant equation given by the form:
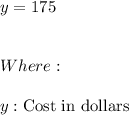
The new plan would charge a flat rate of $94 plus an additional $4.50 per device connected to the network. So the linear equation is:

So we need to find the number of devices, x, for which the cost of the new plan is less than the cost of the current plan. By using inequalities:
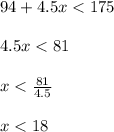
So you should connect less than 18 devices in a month in order for the cost of the new plan to be less than the cost of the current plan.