Answer:
Part a) The number is 18
Part b) The number is 32
Explanation:
Let
x ----> tens digit
y ---> unit digits
N ----> the number (xy)
Part a) Find the two-digit number which is 2 times the sum of its digits
we know that
The number is equal to
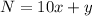 ----> equation A
----> equation A
Remember that
The two-digit number is 2 times the sum of its digits
so
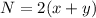 -----> equation B
-----> equation B
equate equation A and equation B
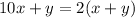
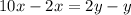
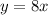
The only single-digit values for x and y that satisfy the requirements are
x=1, y=8
therefore
The number is 18
Part b) Find the two-digit number which is greater than the product of its digits by 26
we know that
The number is equal to
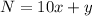 ----> equation A
----> equation A
Remember that
The two-digit number is greater than the product of its digits by 26
so
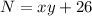 -----> equation B
-----> equation B
equate equation A and equation B

Subtract xy from each side
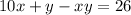
Factor -y

X must be bigger than 2 or we cannot get 26
Let x=3
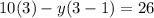
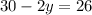
Subtract 30 from each side

Divide by -2 both sides
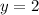
therefore
The number is 32