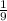Answer:
Explanation:
Let the numbers be x,y, where x>y
The geometric mean is
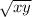
The Arithmetic mean is
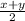
The ratio of the geometric mean and arithmetic mean of two numbers is 3:5.
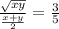
We can write the equation;
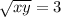
or
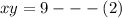
l
and
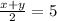
or
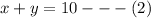
Make y the subject in equation 2
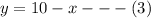
Put equation 3 in 1
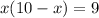
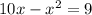

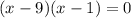
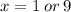
When x=1, y=10-1=9
When x=9, y=10-9=1
Therefore x=9, and y=1
The ratio of the smaller number to the larger number is