Question

Two toy cars are put on a downhill ramp. One car, Car A, travels at a speed represented as y = 6x, where y is the number of meters traveled and x is the number of seconds. The distances and times of the second car, Car B, are shown in the following table.

Answer 1

Step-by-step explanation:

Step-by-step explanation:

Hello! don't forget to write complete questions in order to get good and exact answers. You haven't provided any table, so I'll assume this one:

`\begin{array}{cc}x(seconds) & y(meters)\\0 & 0\\1 & 10\\2 & 20\end{array}`

The speed of this can is the slope of the line given by the table, therefore:

`s_(B):\text{speed of car B} \\m:slope\\ \\ \\s_(B)=m=(10-0)/(1-0)=10m/s`

From the table, we know that the line passes through the origin, so the equation is:

`y=10x`

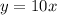
For car A, we know that the speed is also the slope of that line, so:

`S_(A):\text{Speed of car A} \\ \\ s_(A)=m=6m/s`

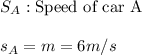
By comparing these two values, we can conclude that:

Car b is faster by 4 meters per second