Question

Match the y-coordinate with the given x-coordinate for the equation y = log2x.

1. 8
1
2. 4
3
3. 2
2
4. 1
-1
5. 1/2
0

Answer 1

1. 8

1

3

2. 2

3

0

3. 1

5

-1

4. 4

4

2

5. 1/2

2

1

Answer 2

If we evaluate the function
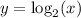`y=\log_2(x)` at the given points, we have:

`\log_2(8)=3`

`\log_2(4)=2`

`\log_2(2)=1`

`\log_2(1)=0`

`\log_2\left((1)/(2)\right)=-1`

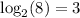
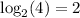
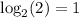
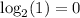
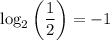
In fact, the function
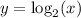`y=\log_2(x)` returns, for a given number
`x`, the exponent you have to give to 2 to obtain
`x`.

So, you want to obtain 8, you have to raise 2 to the 3rd power, if you want 4 you have to raise 2 to the 2nd power, and so on.