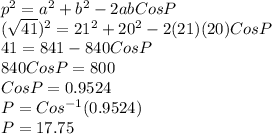Answer:
17.75°
Explanation:
Since it is a right triangle, we can use pythagorean theorem to find the unknown side, side opposite of the angle "?".
Let that side be "x", so we can write (using pythagorean theorem):
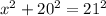
Now, solving for x:
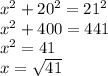
Now we use Law of Cosines to solve for the angle "?".
Law of Cosines:
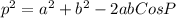
Where
p is the side opposite to angle
P is the angle (we want to solve for)
a, and b are the two sides given
Thus, we have: