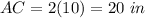Answer:
A)
 and
and
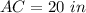
B)
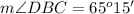 and
and
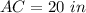
Explanation:
The picture of the question in the attached figure
Problem A
we know that
Triangle ABC has two equal sides
AB ≅
BC
so
Is an isosceles triangle
therefore
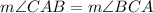
Remember that
The altitude to the base of an isosceles triangle bisects the vertex angle. and bisects the base
In this problem segment BD represent the altitude to the base of an isosceles triangle ABC
so
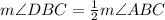
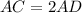
Part 1) Find the measure of angle DBC
we have
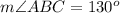
substitute
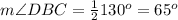
Part 2) Find the value of segment AC
we have
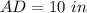
substitute
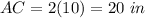
Problem B
we know that
Triangle ABC has two equal sides
AB ≅
BC
so
Is an isosceles triangle
therefore
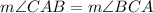
Remember that
The altitude to the base of an isosceles triangle bisects the vertex angle. and bisects the base
In this problem segment BD represent the altitude to the base of an isosceles triangle ABC
so
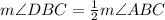
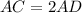
Part 1) Find the measure of angle DBC
we have

substitute

Part 2) Find the value of segment AC
we have
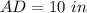
substitute