Question

What is the x-coordinate of the point that divides the directed

line segment from J to k into a ratio of 2:5?
=
-
+
OOOO

Answer 1

The x - coordinate of the point is
`x=-2`

Step-by-step explanation:

Given that the coordinates of the two points J and K are (-6,-2) and (8,-9)

We need to determine the x - coordinate of the point that divides the directed line segment from J to K into a ratio of 2 : 5

The value of the x - coordinate can be determined using the formula,

`x=(m)/(m+n) (x_2-x_1)^2+x_1`

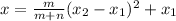
where m = 2, n = 5 and
`x_1=-6` and
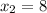`x_2=8` in the above formula, we get,

`x=(2)/(2+5) (8+6)+(-6)`

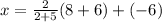
Simplifying, we get,

`x=(2)/(7) (14)-6`

Dividing the terms, we get,

`x=2(2)-6`

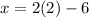
Multiplying the terms, we have,

`x=4-6`

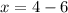
Subtracting, we get,

`x=-2`

Thus, the x - coordinate of the point is
`x=-2`