Question

Cylindrical

Diameter of 14, 40 feet long sketch the tank

Answer 1

Part 1) see the attached figure

Part 2)
`V=1,960\pi\ ft^3` or
`V=6,154.4\ ft^3`

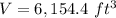
Explanation:

The complete question is

A gas company’s delivery truck has a cylindrical tank that is 14 feet in diameter and 40 feet long.

1. Sketch the tank, and mark the radius and the height.

2. How much gas can fit in the tank?

Part 1) Sketch the tank, and mark the radius and the height.

we know that

The radius is equal to

`r=14/2=7\ ft` ----> the radius is half the diameter

The height is the same that the long of the cylinder

so

`h=40\ ft`

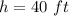
The sketch in the attached figure

Part 2) How much gas can fit in the tank?

we know that

To find out how much gas can fit in the tank, determine the volume of the cylinder

The volume of the cylinder is equal to

`V=\pi r^(2) h`

we have

`r=7\ ft\\h=40\ ft`

substitute

`V=\pi (7)^(2) (40)`

`V=1,960\pi\ ft^3` ----> exact value

assume

`\pi =3.14`

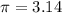
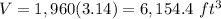`V=1,960(3.14)=6,154.4\ ft^3` ----> approximate value