Question

How would I do this question?​

Answer 1

a) 3

b) S: (½, -15)

Explanation:

a) gradient of the normal at R:

4y + x = 24

y = (-¼)x + 24

Slope of the Normal: -¼

Slope of the tangent at R:

-1 ÷ -¼ = 4

dy/dx = 2kx - 8

4 = 2k(2) - 8

12 = 4k

k = 3

Slope of the tangent: 4

Coordinates of R: (2,y)

y = 3(2)² - 8(2) - 5 = -9

Equation of tangent:

y = 4x + c

-9 = 4(2) + c

c = -17

y = 4x - 17

Point of intersection of tangent and the other curve:

4x - 17 = 4x - (1/x³) - 9

4x⁴ - 17x³ = 4x⁴ - 1 - 9x³

-8x³ = -1

x³ = ⅛

x = ½

y = 4(½) - 17

y = -15

S: (½, -15)

Answer 2

Explanation:

(a)

`y = kx^(2) -8x-5`

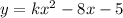
Derivative of the curve is:

`(dy)/(dx) = 2kx - 8`

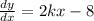
At point R, value of the derivative would be:

`(dy)/(dx)=4k-8`

The derivative of a curve at a point is the slope of the tangent to the curve at that point.

∴Slope of tangent at R = 4k - 8

Now, equation of normal to the curve is: 4y + x = 24;

Convert this in y = mx + c form:

`y = (-x)/(4) + 6`

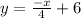
Hence, slope of the normal is: (-1/4)

Now, relation between slope of normal and tangent is:

Slope of tangent = -1/Slope of normal

Substituting the slopes for normal and tangent in this equation we get:

`4k - 8 = (-1)/((-1/4))`

Calculating, k = 3.

(b)

Point R has the x co-ordinate of 2. Since point R lies on the curve with the given equation, it must satisfy the equation.

Hence, substituting the x co-ordinate of R in the equation we get,

`y=4*3-16-5=-9`

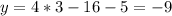
∴R(x,y) ≡ (2, -9)

Now, to find the co-ordinates of point S, the equations of the tangent to the first curve must be known. Let's assume that the equation of tangent is given by:

y = mx + c

Here, m = slope of tangent = 4k - 8 = 4;

Also, this tangent passes through point R, which has x co-ordinate 2. Hence, R must satisfy the equation of the tangent. Hence, substituting co-ordinates of R:

-9 = 4*2 + c

∴ c = -17

Hence, equation of the tangent is:

y = 4x - 17 ;

Now, equating the equation of the tangent and the 2nd curve to find the value of x co -ordinate of S:

`4x - 17 = 4x -(1)/(x^3) - 9`

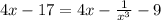
Solving for x: x = 1/2;

Substitute x = 1/2 in eq. of tangent to find the y co-ordinate:

y = 4*(1/2) - 17 = -15

S(x,y) ≡ (1/2,-15)