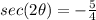Question

Find sec 2Theta in exact value

Answer 1

`sec(2\theta)=-(5)/(4)`

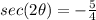
Explanation:

we know that

step 1

Find
`cos(\theta)`

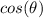
we know that

`tan^2(\theta)+1=sec^2(\theta)`

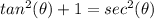
we have

`tan(\theta)=3`

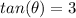
substitute

`3^2+1=sec^2(\theta)`

`sec^2(\theta)=10`

`sec(\theta)=\pm√(10)`

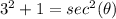
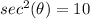
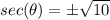
Remember that

Angle theta lie in Quadrant I

so

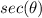`sec(\theta)` is positive

`sec(\theta)=√(10)`

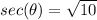
Remember that

`sec(\theta)=(1)/(cos(\theta))`

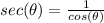
therefore

`cos(\theta)=(1)/(√(10))`

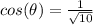
step 2

Find
`sin(\theta)`

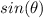
we know that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

`sin(\theta)=tan(\theta)cos(\theta)`

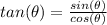
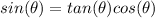
we have

`cos(\theta)=(1)/(√(10))`

`tan(\theta)=3`

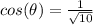
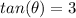
substitute

`sin(\theta)=(3)((1)/(√(10)))`

`sin(\theta)=(3)/(√(10))`

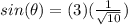
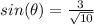
step 3

Find
`cos(2\theta)`

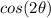
we know that

`cos(2\theta)=2cos^2(\theta)-1`

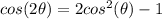
we have

`cos(\theta)=(1)/(√(10))`

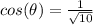
substitute

`cos(2\theta)=2((1)/(√(10)))^2-1`

`cos(2\theta)=(1)/(5)-1`

`cos(2\theta)=-(4)/(5)`

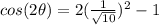
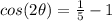
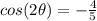
Remember that

`sec(2\theta)=(1)/(cos(2\theta))`

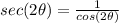
therefore

`sec(2\theta)=-(5)/(4)`