The product would expand to
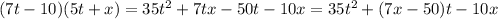
This is a trinomial, and the only way to make it a binomial is to cancel out a coefficient using our variable
 .
.
So, we can cancel either the linear term or the constant term.
In the first case, we require

In the second case, we require
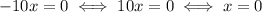
But
 must be a non-zero rational number, so this solution is not feasible.
must be a non-zero rational number, so this solution is not feasible.