Answer:
The answers to the questions are;
1. null hypothesis is μ = 9.5
alternative hypothesis is μ < 9.5
2. The null hypothesis is μ = 8.96
alternative hypothesis is μ < 8.96
3. The test statistic for the test t = -4
4. We accept the null hypothesis that the mean remain the same and we reject the alternative hypothesis that the mean has changed.
Explanation:
To solve the question, we note that the farmer would like to know if the apples have growing smaller at the current season therefore;
1. The null hypothesis is μ = 9.5
The alternative hypothesis is μ < 9.5
2. Action limits are the minimum and maximum values of acceptability and it s derived by
Action limit = Average ± 3 × Standard deviation
= 9.5 ± 3 × 0.18 = Upper limit = 10.04
Lower limit = 8.96
Using the action limit for decision rule since we have inclement weather, our limit should be the lower limit of 8.96 and the null and alternative hypothesis becomes
The null hypothesis is μ = 8.96
The alternative hypothesis is μ < 8.96
3. The test statistic is given by
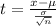
Where:
x' = Sample mean = 9.320
μ = Population mean = 9.500
σ = Standard deviation = 0.18
n = Number of data = 16
Therefore t =
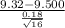 = -4
= -4
The test statistic for the test t = -4
4. The conclusion of the test is
At a significance level a = 0.05, z
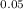 = 1.645 from normal distribution tables
= 1.645 from normal distribution tables
Therefore since the test statistic is -4 we accept it where z < -z
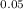
hence since -4 < -1.645, we accept the null hypothesis that the mean remain the same.