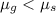Question

When a board with a box on it is slowly tilted to a larger and larger angle, common experience shows that the box will at some point "break loose" and start to accelerate down the board. The box begins to slide once the component of its weight parallel to the board, , equals the maximum force of static friction. Which of the following is the most general explanation for why the box accelerates down the board after it begins to slide (rather than sliding with constant speed)?

a. Once the box is moving, w|| is greater than the force of static friction but less than the force of kinetic friction.
b. Once the box is moving, w|| is less than the force of static friction but greater than the force of kinetic friction.
c. The coefficient of kinetic friction is less than the coefficient of static friction.
d. When the box is stationary, w|| equals the force of static friction, but once the box starts moving, the sliding reduces the normal force, which in turn reduces the friction.

Answer 1

c. The coefficient of kinetic friction is less than the coefficient of static friction

Step-by-step explanation:

When the box finally does break loose. Then the component of the box weight which is parallel to the board weight parallel component, is equal to the
`\mu_gn`.

`w_(box)=\mu_gn`

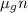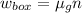
For the box to acce;erate thee must be non-zero net force acting on the box parallel to the board. Or we can say,

`w_1>f_g\\w_1>\mu_gn`

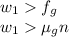
Therefore the force of kinetic friction must be less than the force of static friction. Thus,

`\mu_g<\mu_s`