Question

A boiler has five identical relief valves. The probability that any particular valve will open on demand is 0.92. Assume independent operation of the valves. Calculate P(at least one valve opens). (Round your answer to eight decimal places.)

Answer 1

P(at least one valve opens) = 0.67232.

Explanation:

We are given that a boiler has five identical relief valves. The probability that any particular valve will open on demand is 0.92. Assume independent operation of the valves.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

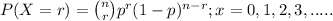
where, n = number of trials (samples) taken = 5 identical relief valves

r = number of success = at least one valve opens

p = probability of success which in our question is probability that

any particular valve will open on demand, i.e; 0.92

LET X = Number of valve opens on demand

So, it means X ~
`Binom(n=5, p=0.92)`

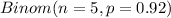
Now, Probability that at least one valve opens is given by = P(X
`\geq` 1)

P(X
`\geq` 1) = 1 - Probability that no valve opens

= 1 - P(X = 0)

= 1 -
`\binom{5}{0}0.92^(0) (1-0.92)^(5-0)`

=
`1-(1 * 1 * 0.08^(5))`

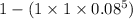
= 1 - 0.32768 = 0.67232

Therefore, Probability that at least one valve opens is 0.67232.