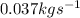Question

Benzene gas (C6H6) at 25° C and 1 atm, enters a combustion chamber operating at steady state and burns with 95% theoretical air entering at 25° C and 1 atm. The combustion products exit at 1000 K and include only CO2 , CO , H2O , and N2.

Determine:
The mass flow rate of the fuel, in kg/s, to provide heat transfer at a rate of 1000 kW

Answer 1

The mass flow rate of the fuel, in kg/s =
`0.037 kgs^(-1)`

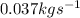
Step-by-step explanation:

The actual balanced equation for the combustion reaction can be written as :

`C_6H_6 +(7.5)(O_2+3.76N_2) ------> 6CO_2 +3H_2O+28.2N_2`

At 95% theoretical air entering at 25° C and 1 atm, the equation of the reaction can be represented as :

`C_6H_6 + 7.125(O_2+3.76N_2) ------> 5.25 CO_2+ 0.75CO+3H_2O+26.79N_2`

The Energy rate formula can be use to determine the mass flow rate of the fuel and which is given as:

`(Q_(Cv))/(n_(fuel))} = 5.25( \bar h_f^0 + \delta \bar h)_(co_2) + 0.75 (\bar h^0_f +\delta \bar h )_(co) +3( \bar h_f^0 + \delta \bar h)_(H_2O) + 26.79( \bar h_f^0 + \delta \bar h)_(N_2)- (\bar h_f^0)_(fuel)`

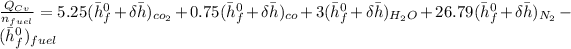
from ideal gas table at respective amount for each compound; we have:

`(Q_(Cv))/(n_(fuel))} = 5.25 (-393520 + 42769-9364) + 0.75 (-110530+30355-8664 ) +3(-241820+35882-9904) + 26.79( 30129-8669)-82930`

`(Q_(Cv))/(n_(fuel))} = -2112780 kJ/mol.k`

`n_(fuel) = (Q_(cv))/(-2112780kJ/kmol)`

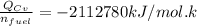
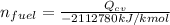
Given that;

The combustion products exit at 1000 K =
`Q_(cv)`

`n_(fuel)= (-1000)/(-2112780)`

`n_(fuel)= 4.73*10^(-3) kmol/s`

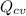
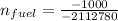
From the ideal gas tables M = 78.11 kg/kmol

∴

`n_(fuel)= 4.73*10^(-3) kmol/s * 78.11 kg/kmol`

`n_(fuel) = 0.037 kgs^(-1)`

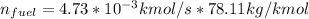
∴ The mass flow rate of the fuel, in kg/s =
`0.037 kgs^(-1)`