Question

Steel rods are manufactured with a mean length of 21 centimeter​(cm). Because of variability in the manufacturing​ process, the lengths of the rods are approximately normally distributed with a standard deviation of 0.05 cm. ​(

a) What proportion of rods has a length less than 20.9 ​cm?​(Round to four decimal places as​ needed.)
(b) Any rods that are shorter than 20.88 cm or longer than 21.12 cm are discarded. What proportion of rods will be​ discarded?​(Round to four decimal places as​ needed.) ​
(c) Using the results of part​ (b), if 5000 rods are manufactured in a​ day, how many should the plant manager expect to​ discard? ​(Use the answer from part b to find this answer. Round to the nearest integer as​ needed.)
​(d) If an order comes in for 10000 steel​ rods, how many rods should the plant manager expect to manufacture if the order states that all rods must be between 20.9 cm and 21.1 ​cm?

Answer 1

a) 0.0228

b) 0.0164 = 1.64% of rods will be​ discarded.

c) The plant manager should expect to discard 82 rods.

d) The plant manager should expect to manufacture 9544 rods.

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

`\mu = 21, \sigma = 0.05`

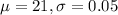
a) What proportion of rods has a length less than 20.9 ​cm?

This is the pvalue of Z when X = 20.9. So

`Z = (X - \mu)/(\sigma)`

`Z = (20.9 - 21)/(0.05)`

`Z = -2`

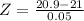
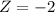
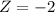`Z = -2` has a pvalue of 0.0228

0.0228 = 2.28% of rods have a length less than 20.9 ​cm.

(b) Any rods that are shorter than 20.88 cm or longer than 21.12 cm are discarded. What proportion of rods will be​ discarded?​(

Shorter than 20.88

pvalue of Z when X = 20.88

`Z = (X - \mu)/(\sigma)`

`Z = (20.88 - 21)/(0.05)`

`Z = -2.4`

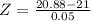
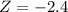
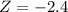`Z = -2.4` has a pvalue of 0.0082.

Longer than 21.12

1 subtracted by the pvalue of Z when X = 21.12

`Z = (X - \mu)/(\sigma)`

`Z = (21.12 - 21)/(0.05)`

`Z = 2.4`

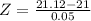
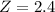
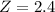`Z = 2.4` has a pvalue of 0.9918

1 - 0.9918 = 0.0082

2*0.0082 = 0.0164

0.0164 = 1.64% of rods will be​ discarded.

(c) Using the results of part​ (b), if 5000 rods are manufactured in a​ day, how many should the plant manager expect to​ discard?

1.64% of 5000. So

0.0164*5000 = 82

The plant manager should expect to discard 82 rods.

​(d) If an order comes in for 10000 steel​ rods, how many rods should the plant manager expect to manufacture if the order states that all rods must be between 20.9 cm and 21.1 ​cm?

Proportion of rods between 20.9 cm and 21.1cm is the pvalue of Z when X = 21.1 subtracted by the pvalue of Z when X = 20.9. So

X = 21.1

`Z = (X - \mu)/(\sigma)`

`Z = (21.1 - 21)/(0.05)`

`Z = 2`

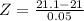
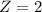
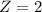`Z = 2` has a pvalue of 0.9772

X = 20.9

`Z = (X - \mu)/(\sigma)`

`Z = (20.9 - 21)/(0.05)`

`Z = -2`

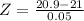
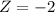
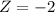`Z = -2` has a pvalue of 0.0228

0.9772 - 0.0228 = 0.9544

Out of 10,000

0.9544*10000 = 9544

The plant manager should expect to manufacture 9544 rods.