Answer:
B. $163 and $171
Explanation:
from the question, we were given the following:
mean= $167
standard deviation, =$40
sample size, n = 100
significance level, α= i- confidence level= 1- 0.95=0.05
from the z table, we get;
critical value,
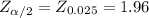
error margin = critical value ×
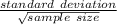
= 1.96×
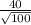 = 7.84
= 7.84
thus lower limit = mean - error margin = $167 - $7.84 =159.16
the upper limit = mean + error margin = $167 + $7.84 = $174.84
the closest is B. $163 and $171