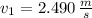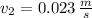Question

A 65.8-kg person throws a 0.0413 kg snowball forward with a ground speed of 32.5 m/s. A second person, with a mass of 58.7 kg, catches the snowball. Both people are on skates. The first person is initially moving forward with a speed of 2.51 m/s, and the second person is initially at rest. (Disregard the friction between the skates and the ice.)

What are the velocities of the two people after the snowball is exchanged?

Answer 1

`v_(1) = 2.490\,(m)/(s)`

`v_(2) = 0.023\,(m)/(s)`

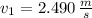
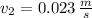
Step-by-step explanation:

The statement is described physically by means of the Principle of Momentum Conservation. Let assume that first person moves in the positive direction:

First Person

`(65.8\,kg)\cdot (2.51\,(m)/(s)) = (65.8\,kg)\cdot v_(1) + (0.0413\,kg)\cdot (32.5\,(m)/(s) )`

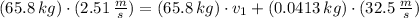
Second Person

`(0.0413\,kg)\cdot (32.5\,(m)/(s))+(58.7\,kg)\cdot (0\,(m)/(s))=(0.0413\,kg+58.7\,kg)\cdot v_(2)`

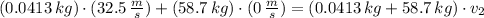
The final velocities of the two people after the snowball is exchanged is:

`v_(1) = 2.490\,(m)/(s)`

`v_(2) = 0.023\,(m)/(s)`