Question

The CEO of the Jen and Benny's ice cream company is concerned about the net weight of ice cream in their 50 ounce ice cream tubs. He decides that he wants to be fairly sure that the mean weight of these ice cream tubs (?) is greater than 52 ounces. A hypothesis test is conducted with the following hypotheses:

H0: u = 52

Ha: u > 52

The level of significance used in this test is ? = 0.05. A random sample of 26 ice cream tubs are collected and weighed. The sample mean weight is calculated to be x = 55.45 and the sample standard deviation is s = 9.78. You may find this Student's t distribution table useful throughout this question.

a)Calculate the test statistic (t) for this test. Give your answer to 4 decimal places.

t =

b)The result of this test is that the null hypothesis isis not rejected.

Answer 1

(a) Test statistics (t) = 1.7987

(b) The result of this test is that the null hypothesis is rejected.

Explanation:

We are given that a random sample of 26 ice cream tubs are collected and weighed. The sample mean weight is calculated to be
`\bar X` = 55.45 and the sample standard deviation is s = 9.78.

Null Hypothesis,
`H_0` :
`\mu` = 52 {means that the mean weight of these ice cream tubs is greater than 52 ounces}

Alternate Hypothesis,
`H_1` :
`\mu` > 52 {mean that the mean weight of these ice cream tubs is greater than 52 ounces}

(a) The test statistics that will be used here is One sample t-test statistics;

T.S. =
`(Xbar-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

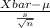where,
`\bar X` = sample mean weight = 55.45

s = sample standard deviation = 9.78

n = sample of ice cream tubs = 26

So, test statistics =
`(55.45-52)/((9.78)/(√(26) ) )` ~
`t_2_5`

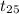
= 1.7987

Therefore, test statistics (t) is 1.7987.

(b) Now, at 0.05 significance level, the t table gives critical value of 1.708. Since our test statistics is more than the critical value of t which means our test statistics will fall in the rejection region and we have sufficient evidence to reject our null hypothesis.

Therefore, the result of the test is that the null hypothesis is rejected and we conclude that the mean weight of these ice cream tubs is greater than 52 ounces.