Question

1. The angular velocity of a fan blade is 8.4 radians per second.

Approximately how many revolutions does the fan blade make in 1.4 minutes?

Enter your answer, rounded to the nearest tenth of a revolution, in the box.
_____________________________________________________________
2. Two wheel gears are connected by a chain. The larger gear has a radius of 8 centimeters and the smaller gear has a radius of 3 centimeters. The smaller gear completes 24 revolutions in 20 seconds.

What is the linear velocity of each of the gears in centimeters per minute?

A. The linear velocity of the smaller gear is 144π centimeters per minute. The linear velocity of the larger gear is 54π centimeters per minute.

B. The linear velocity of the gears is the same. The linear velocity is 432π centimeters per minute.

C. The linear velocity of the gears is the same. The linear velocity is 7.2π centimeters per minute.

D. The linear velocity of the smaller gear is 432π centimeters per minute. The linear velocity of the larger gear is 144π centimeters per minute.

Answer 1

1. The fan blade makes 112.3 revolutions in 1.4 minutes

2. The linear velocity of the gears is the same. The linear velocity is 432π centimeters per minute ⇒ B

Explanation:

1.

∵ The angular velocity of a fan blade is 8.4 radians per second

∴ ω = 8.4 rad/sec

- The revolution = the product of angular velocity and the time

of revolution ÷ 2π

∵ Revolutions = (ω . t)/2π

∵ The fan blade makes x revolutions in 1.4 minutes

∴ t = 1.4 minutes

- Change it to seconds

∵ 1 minute = 60 seconds

∴ 1.4 minutes = 1.4 × 60 = 84 seconds

- Substitute ω and t in the rule of revolutions

∴ Revolutions =
`((8.4)(84))/(2\pi )`

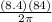
∴ Revolutions ≅ 112.2997278

∴ Revolutions ≅ 112.3

- Round it to the nearest tenth

∴ The fan blade makes 112.3 revolutions in 1.4 minutes

2.

∵ The radius of the larger gear is 8 centimeters

∵ The radius of the small gear is 3 centimeters

∵ The two gears are connected by a chain

- That means the move the same distance together

∴
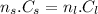`n_(s).C_(s)=n_(l).C_(l)` , where n is the number of revolution for each

gear and C is the circumference of each gear

The formula of the circumference of a circle is C = 2πr

∵
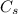`C_(s)` = 2π(3) = 6π

∵
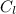`C_(l)` = 2π(8) = 16π

∵ The smaller gear completes 24 revolutions in 20 seconds

∴
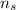`n_(s)` = 24

- Substitute them in the rule above to find
`n_(l)`

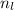
∵ 24 × 6π =
`n_(l)` × 16π

∴ 144π =
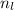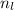`n_(l)` × 16π

- Divide both sides by 16π

∴ 9 =
`n_(l)`

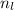
∴ The larger gear completes 9 revolutions in 20 seconds

The linear velocities of the two gears are equal because they move together and make the same distance in the same time

∵ The linear velocity = Distance ÷ Time

∵ Distance which each gear makes = C × n

∴ V =
`(nC)/(t)`

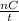
Let us use the smaller gear to find the linear velocity

∵ C = 6π centimeters

∵ n = 24 revolution

∵ t = 20 seconds

- Change it to minutes

∴ 20 seconds = 20 ÷ 60 =
`(1)/(3)` minute

∴ V =
`((24)(6\pi ))/((1)/(3))`

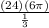
∴ V = 432π cm/min

Let us check the answer by find the linear velocity fro the larger gear

∵ C = 16π centimeters

∵ n = 9 revolution

∵ t =
`(1)/(3)` minute

∴ V =
`((9)(16\pi ))/((1)/(3))`

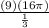
∴ V = 432π cm/min

The linear velocity of the gears is the same. The linear velocity is 432π centimeters per minute