Answer:
See below for answers and explanations
Explanation:
Problem 1
First, identify the three vectors in component form (remember to have the direction angle for each vector account for the quadrants they are in!):
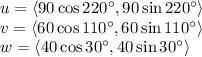
Secondly, we add them:
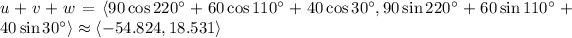
Thirdly, find the magnitude of the new vector:
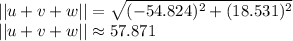
And finally, find the direction of the new vector:
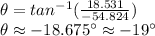
Because our new vector is in Quadrant II, our found direction angle is a reference angle, telling us that the actual direction of our vector is 19° clockwise from the negative x-axis, which would be 180°-19°=161°
Thus, B is the best answer
Problem 2
To find the component form of a vector, we simply subtract the initial point from the terminal point. In this case, our initial point is at (7,-1) and our terminal point is at (1,6). We subtract the horizontal and vertical components separately:

Thus, A is the correct answer
Problem 3
Again, subtract the initial point from the terminal point to find the vector, and then apply scalar multiplication:
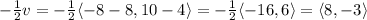
Thus, C is the correct answer
Problem 4 (top one in 4th image)
Remember that scalar multiplication only affects the magnitude of the vector and not the direction. Thus,
![-3u=-3\bigr[20\langle\cos30^\circ,\sin30^\circ\rangle\bigr]=-60\langle\cos30^\circ,\sin30^\circ\rangle](https://img.qammunity.org/2023/formulas/mathematics/college/thtgfm8flei9k873xiks3g52z8dejwz8dh.png) , which means our magnitude is -60 and our direction remains 30°.
, which means our magnitude is -60 and our direction remains 30°.
Thus, B is the correct answer
Problem 5 (fake #6, bottom one in 4th image)
Basically, whatever is in front of the i represents the horizontal component, and whatever is in front of the j represents the vertical component, so:
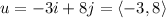
Thus, B is the correct answer
Problem 6 (real one, 5th image)
Recall:
- Two vectors are said to be orthogonal if their dot product is 0 and are perpendicular to each other (form a 90° angle)
- Two vectors are said to be parallel if the angle between the vectors is 0° or 180° i.e. cosθ=-1
Knowing these facts, let us compute the dot product:

Since the dot product of the two vectors is not 0, then the vectors are not orthogonal, so we can eliminate choices A and B
To check if the vectors are parallel, find the angle between them:

So, since the angle between the two vectors is 180°, this implies that cosθ=-1, and the two vectors must be parallel.
Thus, D is the correct answer