Option A: 4 is the length of PE
Step-by-step explanation:
Given that PA=6, PD=4, and BE=5
We need to determine the length of PE
The length of PE can be determined using the intersecting secant tangent theorem.
Applying the secant tangent theorem, we get,
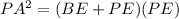
Substituting the values of the PA and BE, we get,
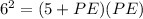
Simplifying, we get,
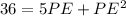
Subtracting both sides of the equation by 36, we get,

Switch sides, we get,
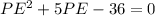
Solving this equation, we get,
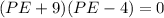
Equating each term equal to zero, we get,
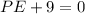 and
and
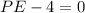
Simplifying, we get,
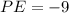 and
and
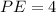
The value of PE cannot be negative.
Thus, the length of PE is 4.
Hence, Option A is the correct answer.