Question

Quadrilateral ABCD is reflected over the x-axis to create quadrilateral A'B'C'D!

What are the coordinates of A'and B'?
A) A' (-6, -2)
B'(-6,-5)
B) A' (2-6)
B'(5.-6)
O C) A' (6, -2)
B' (6,5)
OD) A' (6, -2)
B'(-6, -5)

Answer 1

The answer is option A the points are
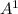`A^(1)` (-6, -2) and
`B^(1)` (-6, -5).

Explanation:

Step 1:

To understand reflection across an axis we need to be able to know which quadrant the shape is already in and in which quadrant it will be in after reflection.

The given shape is currently in the second quadrant where the points in it will have a negative x coordinate and a positive y coordinate. So assume the values are in the format of (-x, y).

Step 2:

Due to reflection across the x-axis, the shape will be reflected on to the third quadrant. In this, the x and y coordinates both have a negative value.

So due to reflection, the x value remains constant and the y value remains the same but both have the opposite symbol i.e. negative.

Step 3:

So (-x, y) becomes (-x, -y).

A (-6, 2) becomes
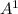`A^(1)` (-6, -2),

B (-6, 5) becomes
`B^(1)` (-6, -5),

C (-3, 4) becomes
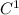`C^(1)` (-3, -4),

D (-2.5, 2) becomes
`D^(1)` (-2.5, 2).

So the points are
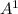`A^(1)` (-6, -2) and
`B^(1)` (-6, -5). This is option A.