Question

Water evaporating from a pond does so as if it were diffusing across an air film 0.15 cm thick. The diffusion coefficient of water in 20 C air is about 0.25 cm2/sec. If the air out of the film is fifty percent saturated, how fast will the water level drop in a day

Answer 1

1.25 cm/day

Step-by-step explanation:

An air thickness , (l) = 0.15 cm

Air Temperature =

`(T_a)=20^0C = (20+273)K\\(T_a)=293K`

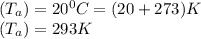
Mass Diffusion coefficient (D) =
`0.25cm^2/sec`

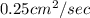
If the air pressure
`(P_a) = 0.5 P_(sat)`

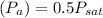
We are to determine how fast will the water
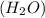`(H_2O)` level drop in a day.

From the property of air at T = 20° C

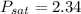`P_(sat) = 2.34` from saturated water properties.

The mass flow of
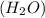`(H_2O)` can be calculated as:

`H_2O = (D)/(\phi) \delta C`

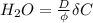
where:

`\delta C = (P_(sat)*P_a)/(RT )`

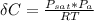
R(constant) = 8.314 kJ/mol.K

`\delta C = (2.34*0.5)/(8.314*293 )`

`\delta C = 4.803*10^(-4)\\ \delta C =0.48*10^(-3) mol/m^3\\ \delta C = 0.48*10^(-6) mol/cm^3`

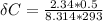
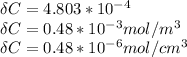
Since 1 mole = 18 cm ³ of water

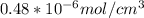`0.48*10^(-6)mol/cm^3` will be:
`(0.48*10^(-6)mol/cm^3 *18)cm^3/cm^3`

`\delta C = 8.64 * 10^(-6)`

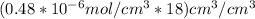
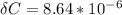
Again:

`H_2O = (D)/(\phi) \delta C`

`= (0.25)/(0.15)*8.69*10^(-6) (cm^2/sec)/(cm)`

`=1.4481*10^(-5) (cm^2/sec)/(cm)`

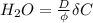
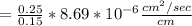
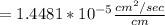
Converting the above value to cm/day: we have:

`1.448*10^(-5)*3600*24(cm)/(s)*(s)/(yr)*(yr)/(day)`

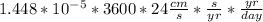
= 1.25 cm/day

∴ the rate at which the water level drop in a day = 1.25 cm/day