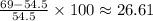Question

A cylindrical metal specimen having an original diameter of 10.55 mm and gauge length of 54.5 mm is pulled in tension until fracture occurs. The diameter at the point of fracture is 7.16 mm, and the fractured gauge length is 69.0 mm. Calculate the ductility in terms of (a) percent reduction in area (percent RA), and (b) percent elongation (percent EL).

Answer 1

(a) 53.94%

(b) 26.61%

Step-by-step explanation:

Change in area will be given by

`\triangle A=\frac {\pi(R_o^(2)-r_n^(2))}{\pi R_o^(2)}` where
`\triangle A` represent change in area R is radius and subscripts O and n represent original and new respectively.

Substituting 10.55/2 for original radius and 7.16/2 for new radius then

`\triangle A=\frac {\pi(5.275^(2)-3.58^(2))}{\pi 5.275^(2)}* 100\approx 53.94`

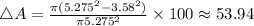
(b)

Similarly, percentage elongation will be found by dividing the change in length by the the original length. In this case, rhe original length was 54.5mm and goes to 69 mm so the change in length is given by subtracting the final length from the original length

Percentage elongation is
`\frac {69-54.5}{54.5}* 100\approx 26.61`