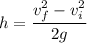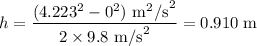Question

A rubber ball with a mass of 0.175 kg is dropped from rest. From what height (in m) was the ball dropped, if the magnitude of the ball's momentum is 0.740 kg · m/s just before it lands on the ground?

Answer 1

Answer: The was dropped from a height of 0.912m

Explanation: Please see the attachments below

Answer 2

0.910 m

Step-by-step explanation:

The momentum of the ball before it hits the ground is its final momentum.

`p_f = mv_f`

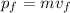
m is the mass of the ball and
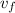`v_f` is the final velocity.

`v_f = (p_f)/(m) = \frac{0.740\text{ kg m/s}}{0.175\text{ kg}} = 4.223\text{ m/s}`

The motion of the ball is under gravity, dropping from rest.

The initial velocity,
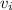`v_i`, is 0 m/s because it is dropped.

Acceleration of gravity, g, is 9.8 m/s².

The height is denoted by h.

We use the equation of motion:

`v_f^2 = v_i^2 + 2gh`

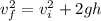
(We are taking g as positive here).

`h= (v_f^2 - v_i^2)/(2g)`

`h= \frac{(4.223^2 - 0^2)\text{ m}^2\text{/s}^2}{2* 9.8\text{ m/s}^2} = 0.910 \text{ m}`