Answer:
The planet has one-fifth of the gravitational acceleration of the Earth.
Step-by-step explanation:
Newton's law of gravitational attraction between two bodies of masses
 and
and
 separated by a distance d gives
separated by a distance d gives
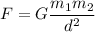 (G is a universal constant)
(G is a universal constant)
For any body of mass m on the Earth surface,

Here, M and R are the mass and the radius of the Earth, respectively.
But this force is the gravitational force on the body.
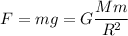
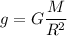
For a planet with 5 times the mass of Earth and 5 times its radius,
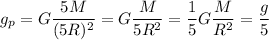
Hence the planet has one-fifth of the gravitational acceleration of the Earth.