Option D:
The expression equivalent to the given expression is 25.
Solution:
The image of the question is attached below.
Given expression:
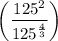
To find which expression is equivalent to the given expression:
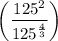
125 can be written as 5 × 5 × 5 = 5³
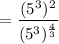
Using the exponent rule:
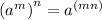
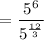
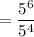
Using the exponent rule:
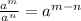
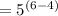
= 5²
= 25
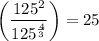
The expression equivalent to the given expression is 25.
Option D is the correct answer.