Explanation:
Given Arithmetic series is:
7+13+19+25+...+ 85
Here,
First term a = 7
Common Difference d = 13 - 7 = 6
last term
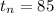
First let us find the number of terms in given series.
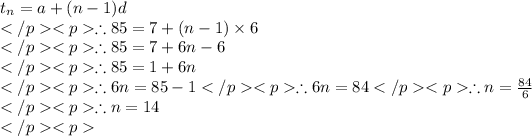
Hence, given series has total 14 terms.
Sum of n terms of an Arithmetic series is given as:
