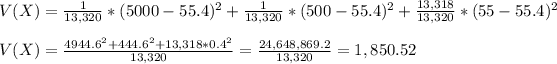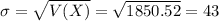Answer:
The expected value of the prize won by a prospective customer receiving a flier os $55.4.
The standard deviation of the value of the prize won by a prospective customer receiving a flier is $43.
Explanation:
The expected value of the prizes is the sum ofthe prizes, weighted by their probability of happening.
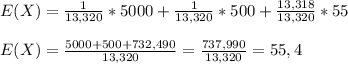
The expected value of the prizes is $55,4.
The standard deviation will be calculated as the square root of the variance: