Question

Use linear approximation to approximate 25.3‾‾‾‾√ as follows. Let f(x)=x√. The equation of the tangent line to f(x) at x=25 can be written in the form y=mx+b. Compute m and b.

Answer 1

Approximation f(25.3)=5.03 (real value=5.0299)

The approximation can be written as f(x)=0.1x+2.5

Explanation:

We have to approximate
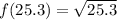`f(25.3)=√(25.3)` with a linear function.

To approximate a function, we can use the Taylor series.

`f(x)=\sum_1^(\infty) (f^((n))(a))/(n!)(x-a)^n`

The point a should be a point where the value of f(a) is known or easy to calculate.

In this case, the appropiate value for a is a=25.

Then we calculate the Taylor series with a number of terms needed to make a linear estimation.

`f(x)\approx f(a)+(f'(a))/(1!)(x-a)`

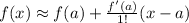
The value of f'(a) needs the first derivate:

`f'(x)=(1)/(2√(x))\\\\f'(a)=f'(25)=(1)/(2√(25))=(1)/(2*5)=(1)/(10)`

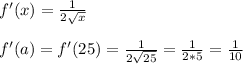
Then

`f(x)\approx f(25)+(1)/(10)(x-25)=√(25) +(1)/(10)(x-25)\\\\f(x)\approx 5+(1)/(10)(x-25)`

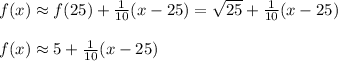
We evaluate for x=25.3

`f(25.3)\approx 5+(1)/(10)(25.3-25)\\\\f(25.3)\approx 5+(1)/(10)(0.3)=5.03`

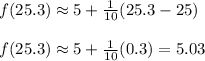
If we rearrange the approximation to be in the form mx+b we have:

`f(x)\approx 5+(1)/(10)(x-25)=5+0.1x-2.5\\\\f(x)\approx 0.1x+2.5`

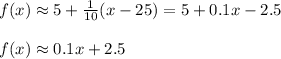
Then, m=0.1 and b=2.5.