Question

A gondola (cable car) at a ski area holds 50 people. Its maximum safe load is 10000 pounds. A population of skiers has a distribution of weights with mean 190 pounds and standard deviation 40 pounds. If 50 skiers are randomly chosen from this population, and take the gondola, what is the probability its maximum safe load will be exceeded

Answer 1

Answer: 0.03855

Explanation:

Given :A population of skiers has a distribution of weights with mean 190 pounds and standard deviation 40 pounds.

Its maximum safe load is 10000 pounds.

Let X denotes the weight of 50 people.

As per given ,

Population mean weight of 50 people =
`\mu=50*190=9500\text{ pounds}`

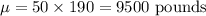
Standard deviation of 50 people
`=\sigma=40√(50)=40(7.07106781187)=282.84`

Then , the probability its maximum safe load will be exceeded =

`P(X>10000)=P((X-\mu)/(\sigma)>(10000-9500)/(282.84))\\\\=P(z>1.7671-8)\\\\=1-P(z\leq1.7678)\ \ \ \ [\because\ P(Z>z)=P(Z\leq z)]\\\\=1-0.96145\ \ \ [\text{ By p-value of table}]\\\\=0.03855`

Thus , the probability its maximum safe load will be exceeded = 0.03855