Answer:
d=0.024m
Step-by-step explanation:
The mass of the isotopes are
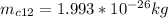
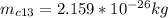
The velocity of isotopes are
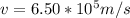
Charge q=+e=1.6×10⁻¹⁹C and the magnetic field is B=0.5700T
The radius of circular paths for isotopes are:

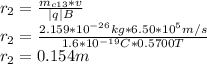
So the spatial separation between two isotopes given as:
d=2r₂-2r₁
d=2(0.154)-2(0.142)
d=0.024m