Question

A mass attached to a spring oscillates with a period of 44 sec. After 33 kg are​ added, the period becomes 55 sec. Assuming that we can neglect any damping or external​ forces, determine how much mass was originally attached to the spring.

Answer 1

Explanation:

Below is an attachment containing the solution.

Answer 2

The mass originally attached to the spring was 58.665 kg

Explanation:

To solve for this we need to consider the equation for a springs oscillating period:

T =
`2*\pi *\sqrt{(m)/(k) }`

Here, m = mass of spring

k = spring constant

Since we know that the period increases by 11 (55 - 44) after the extra weight is added, we have the following equations:

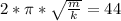`2*\pi *\sqrt{(m)/(k) }=44` -Equation 1

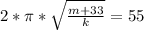`2*\pi *\sqrt{(m+33)/(k) }=55` -Equation 2

solving both equation simultaneously we get:

m = 58.665 kg