Answer: The parchments is 3200 years old.
Explanation: The carbon-14 is radioactive with a half-life (t1/2) of 5730 years. This means that it will take 5730 years for an initial sample of the isotope is reduced to its half. Because of it, Carbon-14 can be used to determine the age of an object.
From the question, "68% as much 14C radioactivity as plant material today" means that there is still 68% of the initial sample of the isotope. To determine how many half-lives passed in that period of time, you use:
A = A₀·
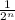 , in which
, in which
A is the amount left after a period of time;
A₀ is the initial amount;
n is the number of half-lives passed in the same period
It's known the remaining amount: A =
 ·A₀.
·A₀.
Substituing and calculating:
 ·A₀ = A₀·
·A₀ = A₀·
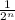
0.68 =
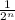
㏑0.68 = ㏑
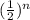
- 0.387 = n·( - 0.693)
n =
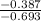
n = 0.558
n is the amount of half-lives passed and it can be written as:
n =
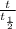 , where:
, where:
t is the period of time;
t1/2 is the half-life;
n =
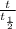
t = n · t1/2
t = 0.558 . 5730
t = 3200 years
The parchment is approximately 3200 years of age.