Question

The radius of a right circular cone is increasing at a rate of 3 inches per second and its height is decreasing at a rate of 3 inches per second. At what rate is the volume of the cone changing when the radius is 40 inches and the height is 30 inches

Answer 1

The volume of cone is increasing at a rate 2512 cubic inches per second.

Explanation:

We are given the following in the question:

`(dr)/(dt) = 3\text{ inches per second}\\\\(dh)/(dt) = -3\text{ inches per second}`

Radius = 40 inches

Height = 30 inches

The volume of cone is given by:

`V = (1)/(3)\pi r^2 h`

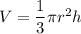
Rate of change of volume is given by:

`(dV)/(dt) = (1)/(3)\pi (2r(dr)/(dt)h+(dh)/(dt)r^2)`

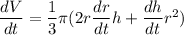
Putting the values, we get,

`(dV)/(dt) = (1)/(3)(3.14) \big(2(40)(3)(30)+(-3)(40)^2\big)\\\\(dV)/(dt) = (1)/(3)(3.14)(2400)\\\\(dV)/(dt) = 2512`

Thus, the volume of cone is increasing at a rate 2512 cubic inches per second.