Answer:
0.875 is the required probability.
Explanation:
We are given the following in the question:
Probability Billy would pass atleast one test = 0.9
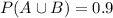
Probability Billy would pass both test = 0.7

The two test are equally difficult.
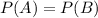
For independent events we can write that
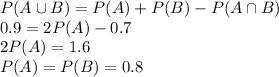
We have to find the conditional probability that Billy passing test 2 given the event that he passes test 1.
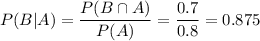
0.875 is the conditional probability of Billy passing test 2 given the event that he passes test 1