Answer:
a)
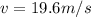
b)
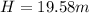
c)
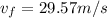
Step-by-step explanation:
a) Let's calculate the work done by the rocket until the thrust ends.
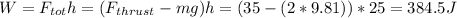
But we know the work is equal to change of kinetic energy, so:

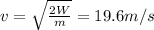
b) Here we have a free fall motion, because there is not external forces acting, that is way we can use the free-fall equations.
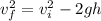
At the maximum height the velocity is 0, so v(f) = 0.

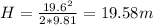
c) Here we can evaluate the motion equation between the rocket at 25 m from the ground and the instant before the rocket touch the ground.
Using the same equation of part b)
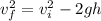
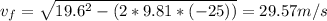
The minus sign of 25 means the zero of the reference system is at the pint when the thrust ends.
I hope it helps you!