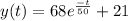Question

The differential equation below models the temperature of an 89°C cup of coffee in a 21°C room, where it is known that the coffee cools at a rate of 1°C per minute when its temperature is 71°C. Solve the differential equation to find an expression for the temperature of the coffee at time t. (Let y be the temperature of the cup of coffee in °C, and let t be the time in minutes, with t = 0 corresponding to the time when the temperature was 89°C.) dy dt = − 1 50 (y − 21)

Answer 1

`y(t) = 68e^{(-t)/(50)}+21`

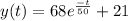
Explanation:

Consider the differential equation
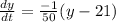`(dy)/(dt)= (-1)/(50)(y-21)`. NOte that this fullfills the condition that the coffee cools down 1°C when y=71°C. We have the initial condition that y(0) = 89°C. Note that this is a separable differential equation, since

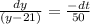`(dy)/((y-21))= (-dt)/(50)` which leads to

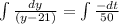`\int(dy)/((y-21))= \int (-dt)/(50)`. This gives us the following result

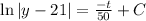`\text{ln}\left|y-21\right| = (-t)/(50)+C` where C is a constant. Then, using the exponential function we have

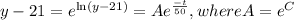`y-21 = e^{\text{ln}(y-21)} = Ae^{(-t)/(50)}, where A = e^(C)` which is another constant.

Given the initial condition, we have that when t=0, y = 89, then

`89-21 = Ae^{(0)/(50)} = A = 68`

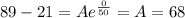
Then, the final solution is

`y(t) = 68e^{(-t)/(50)}+21`