Question

The half-life for the radioactive decay of C-14C-14 is 5730 years. You may want to reference (Pages 598 - 605) Section 14.5 while completing this problem. Part A How long will it take for 25% of the C-14C-14 atoms in a sample of C-14C-14 to decay

Answer 1

Answer: The sample of Carbon-14 isotope will take 2377.9 years to decay it to 25 %

Step-by-step explanation:

The equation used to calculate rate constant from given half life for first order kinetics:

`t_(1/2)=(0.693)/(k)`

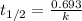
where,

`t_(1/2)` = half life of the reaction = 5730 years

Putting values in above equation, we get:

`k=(0.693)/(5730yrs)=1.21* 10^(-4)yrs^(-1)`

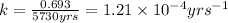
Rate law expression for first order kinetics is given by the equation:

`k=(2.303)/(t)\log([A_o])/([A])`

where,

k = rate constant =
`1.21* 10^(-4)yr^(-1)`

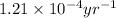
t = time taken for decay process = ? yr

`[A_o]` = initial amount of the sample = 100 grams

[A] = amount left after decay process = (100 - 25) = 75 grams

Putting values in above equation, we get:

`1.21* 10^(-4)=(2.303)/(t)\log(100)/(75)\\\\t=2377.9yrs`

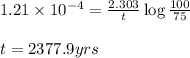
Hence, the sample of Carbon-14 isotope will take 2377.9 years to decay it to 25 %