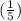P(call a person not from his neighborhood) =
Explanation:
Here, the total number of contacts in the list if Bruce = 25 contacts
The total number of neighbors in the contact = 20 people
Now, let E: Event of calling a person from his neighborhood
So, P(E) =

So, the probability of calling a person from his neighborhood is
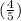
⇒P(E) =
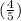
Now,as we know: P(E) + P(not E) = 1
So, the probability of NOT calling a person from neighborhood
= 1 - probability of calling a person from his neighborhood
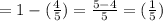
⇒P( not E) =
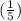
Hence, P(call a person not from his neighborhood) =