Answer:
35.6 seconds
Explanation:
The Poisson distribution has a probability model that follows the given relationship:

For x = zero calls at a probability of 50%, the arrival rate during the call is:
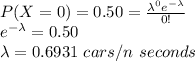
Since cars arrive at a rate of 70 per hour, the length of call 'n' in seconds is:
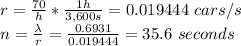
The call should be at most 35.6 seconds long to ensure a 50% probability that no cars arrive during the call.