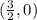For this case we have the following function:

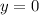 we have:
we have:

Where:
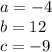
By definition, the discriminant of a quadratic equation is given by:

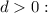 Two different real roots
Two different real roots
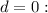 Two equal real roots
Two equal real roots
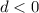 : Two different complex roots
: Two different complex roots
Substituting the values we have:
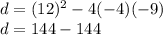
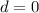
We have two equal real roots.
To find the intersections with the x axis, we do
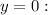

We apply the quadratic formula:
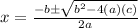
Substituting the values we have:
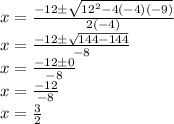
The intersection with the x axis is
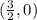
Answer:
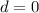
The intersection with the x axis is