Answer:
x=9.5 cm
Step-by-step explanation:
We have here three parts to analyze.
- The first one related to the cylinder A moving to the right with speed v(iA) = 2.0 m/s with the cylinder B at rest, v(iB) = 0.
- The second one, the cylinder A after the collision, whit a velocity v(fA) and cylinder B after the collision whit velocity v(fB).
- The third one, the cylinder B compresses the spring. The velocity of the cylinder B at this moment will be zero.
Let's use conservation of momentum in the first part, to find the one equation:
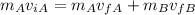 (1)
(1)
Where m(A) = m(B) = 2.2 kg, so the masses canceled out from equation (1):
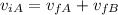
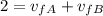 (2)
(2)
We can use the coefficient of restitution to find the second equation:


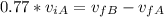
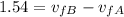 (3)
(3)
We can find v(fA) and v(fB) combining (3) and (4) and solving the system of equations:
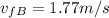
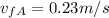
Now, using the conservation of energy, related to the cylinder B, we have:
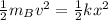 (4)
(4)
here, v is 1.77 m/s.
Solving the equation (4) for x, we have:
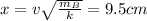
I hope it helps you!